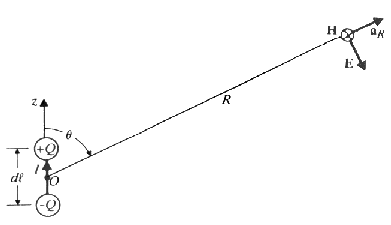
In this chapter we will solve the Maxwell’s equations for a radiating wire and by analyzing the solution we will define the near-field and the far-field. The electromagnetic field radiating from a wire can be calculated by solving Maxwell’s equations for a short current element and then placing the current elements end-to-end.

Figure 3 A small current element or an electric dipole.
To be able to derive the field of a conducting element acting as an electrical dipole, the current in the element is defined to flow along an axis z. This gives that the magnetic vector potential can be expressed as (see Equation 26):
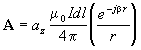 |
Equation 31 |
where:
Equation 32 |
It is wise to use spherical coordinates when deriving the field of a small current element that can be approximated with a point source
Equation 33 |
If A is then expressed in the form
Equation 34 |
it can apparently be divided into the spherical components:
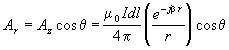 |
|
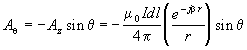 |
Equation 36 |
Equation 37 |
The intensity of the magnetic field is then (using Equation 27):
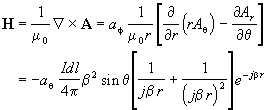 |
Equation 38 |
According to Equation 30 above E can be determined when H is known:
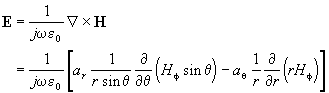 |
Equation 39 |
Which results in:
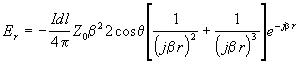 |
Equation 40 |
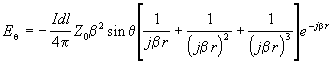 |
Equation 41 |
Equation 42 |
By rewriting those equations we can identify the wavelength and get the following equations in Table 3. A summation of the theory above states that:
If the length of one element is much less than a wavelength (dl << l ) and the element is considered as an oscillating dipole the electric and magnetic fields for one element can, with the use of some algebra, be expressed as:
Table 3 The electric and magnetic field equations for a small oscillating electric dipole
Electric and Magnetic Field Equations for an Electric Dipole |
|
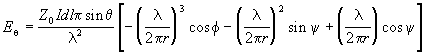 |
|
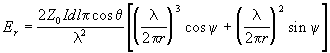 |
|
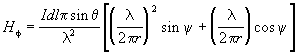 |
|
where:
Analyzing these equations (Equation 43 to Equation 45) we can divide the terms into three different basic terms:
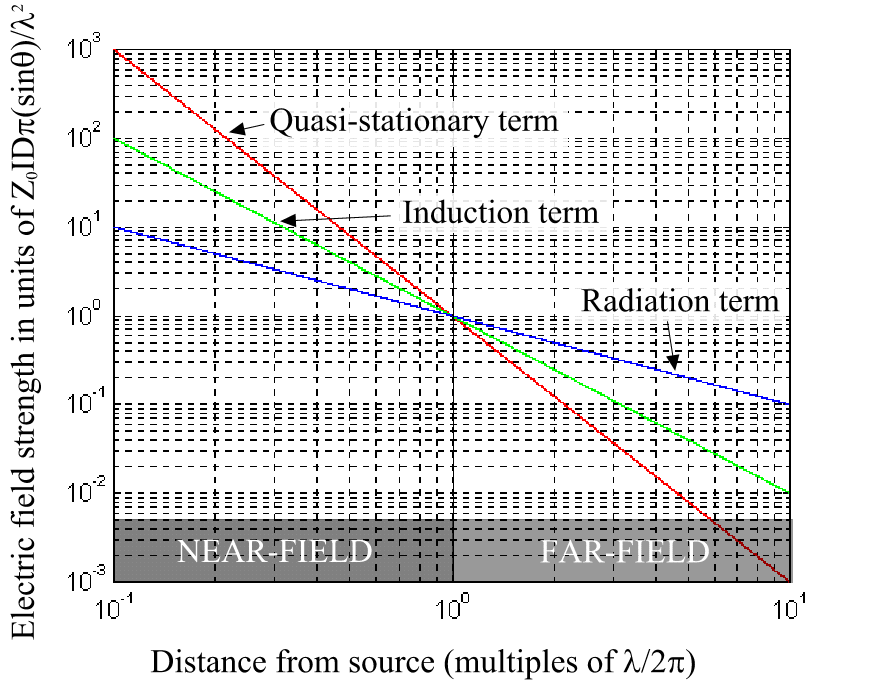
Figure 4 The significance of the different terms for the electric field strength
Notice that all these
terms with the coefficients ![]() ,
, ![]() and
and
![]() will all be equal
(=1) at the distance
will all be equal
(=1) at the distance ![]() . This distance is in this report said to be the
boundary between near-field and far-field and the contributions
from the radiation, induction and the electrostatic term are all
of the same magnitude.
. This distance is in this report said to be the
boundary between near-field and far-field and the contributions
from the radiation, induction and the electrostatic term are all
of the same magnitude.
When r
<< ![]() only the first term in
each equation is significant and will in this case mean that the
wave impedance will be:
only the first term in
each equation is significant and will in this case mean that the
wave impedance will be:
Equation 46 |
that is much greater than the free space impedance Z0 i.e. we will have a high E-field and a low H-field. If the current element had been a current loop with a low circuit impedance instead of the high circuit-impedance of the current element, the first term, or the electrostatic term, in the first two equations (Equation 43 and Equation 44) would disappear and a similar equation would appear in Equation 45. In this case the wave impedance would be:
Equation 47 |
representing a high H-field and a low E-field in the near-field.
When r >> ![]() the last term proportional to r-1 in Equation 43 and Equation 45 will
dominate and the wave impedance will approach the free space
impedance Z0 = 377W . This
is called the far-field or radiation field. The Eq and
the Hf fields will then be in phase and
orthogonal to each other producing plane waves. This is
illustrated in Figure 5 below:
the last term proportional to r-1 in Equation 43 and Equation 45 will
dominate and the wave impedance will approach the free space
impedance Z0 = 377W . This
is called the far-field or radiation field. The Eq and
the Hf fields will then be in phase and
orthogonal to each other producing plane waves. This is
illustrated in Figure 5 below:
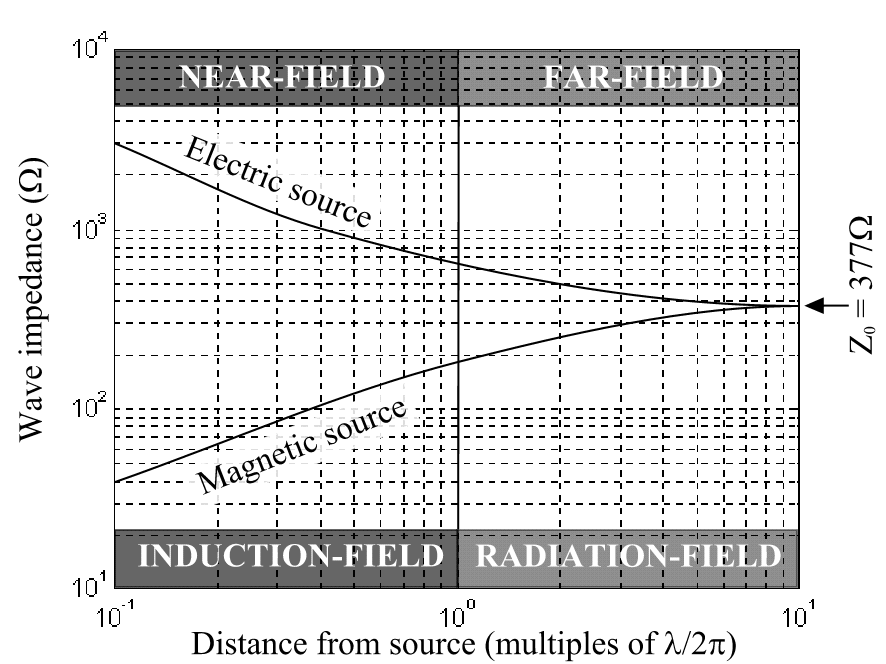
Figure 5 Wave impedance at different distances from either an electric source or a magnetic source
When such current elements are placed end-to-end to produce a model of a radiating wire, the charge at the ends of the elements will cancel and the term due to the electrostatic field (the one proportional to r-3) will disappear. This is however only true with a constant current distribution on the line. With a varying current distribution the electrostatic fields will not cancel entirely. However, if the wire is divided into a sufficient number of segments per wavelength then this error will be small.
The length of telecommunication lines and the size of telecommunication systems are often greater than one wavelength, D ³ l . If the dimension of the field source D is greater than a wavelength the near-field/far-field boundary is said to be at the distance [5]:
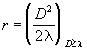 |
Equation 48 |
At a shorter distance maxima and minima would appear due to interference caused by different distances to different parts of the source.
Previous: Maxwell's Equations | Next: Transmission Line
EMC of Telecommunication Lines
A Master Thesis from the Fieldbusters © 1997
Joachim Johansson and Urban Lundgren